Resolución de sistemas con matrices II

- Método de Crammer:

Un sistema de ecuaciones lineales recibe el nombre de sistema de Cramer cuando se cumplen las dos condiciones siguientes:

  1) El número de ecuaciones es igual al número de incógnitas.

  2) El determinante de la matriz de los coeficientes (matriz del sistema) es distinto de cero ( det ( A ) # 0 )

Un sistema de Cramer es, por definición, compatible determinado, puesto que se cumple que rango (A) = rango (A*) = n (nº de incógnitas).

Consideremos un sistema de Cramer, es decir, un sistema de n ecuaciones lineales con  n  incógnitas, cuya expresión general es la siguiente:

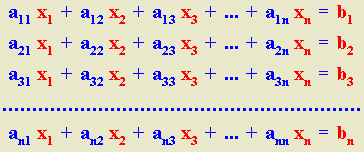
Todos los sistemas de Cramer son compatibles determinados. El valor de cada incógnita se obtiene dividiendo el determinante de la matriz asociada a dicha incógnita por la matriz del sistema (matriz de los coeficientes de las incógnitas). 

Para calcular cada variable hacemos el cociente entre el determinante resultante de sustituir la columna de la variable por la columna de términos independientes. Las otras dos columnas las dejamos como están, dividido todo entre el determinante de A.

   Ejemplo:

Un sistema de Cramer es, por definición, compatible determinado. Pero, ¿Se puede aplicar la regla de Cramer para resolver sistemas de ecuaciones lineales compatibles indeterminados?

La respuesta es también afirmativa. El procedimiento a seguir es el siguiente: Supongamos que tenemos un sistema de  m  ecuaciones lineales con  n  incógnitas, tal que:  rango (A) = rango (A*) = k < n. Por lo tanto, sobran  m - k  ecuaciones y, además, hay  n - k  incógnitas no principales. Para averiguar cuáles son las ecuaciones de las que podemos prescindir, y cuáles son las incógnitas no principales, basta encontrar en la matriz de los coeficientes ( A ) un menor de orden  k  distinto de cero, por ejemplo, el que utilizamos para averiguar el rango de la matriz  A. Las filas que intervienen en este menor son las que corresponden a las ecuaciones principales o independientes. Las restantes ecuaciones las podemos suprimir. Las columnas que figuran en dicho menor corresponden a las incógnitas principales. Las incógnitas no principales las pasamos al otro miembro y pasan a formar un único término junto con el término independiente. Se obtiene, de este modo, un sistema de  k  ecuaciones lineales con  k  incógnitas, cuyas soluciones van a depender de  n - k  parámetros (correspondientes a las incógnitas no principales).

- Teorema de Rouché:

Permite conocer si un sistema de ecuaciones tiene solución a partir del estudio del 
rango de la matriz asociada al sistema (matriz de coeficientes A) y del rango de la matriz 
ampliada de éste (matriz B). 

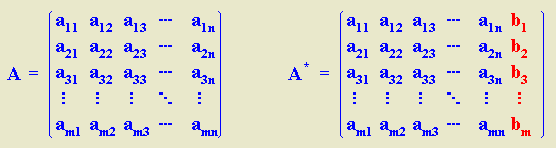
Sea A la matriz de coeficiente asociada a un sistema lineal de n.
Sea A* la matriz ampliada de dicho sistema, se cumple q:
  1) Si Rg (A) no es igual  a Rg (A*): S.I. (no existe solución)
  2) Si Rg (A)=Rg (A*)=n: S.C.D. (existe una única solución)
  3) Si Rg (A)=Rg (A*)<n: S.C.I. (existe infinitas soluciones)

Un caso particular es el de los sistemas homogéneos, es decir, aquellos en los que todos los términos independientes son nulos. Pues, en este caso, las matrices  A  y  A*  son  semejantes a efectos del cálculo del rango, dado que la matriz  A*  es la matriz  A  a la que se le añade una columna de ceros, que podemos suprimir para calcular el rango. Por lo tanto, siempre se cumple que rango (A) = rango (A*). Esto quiere decir que todos los sistemas homogéneos son siempre compatibles. Se cumple:

  1) Si rango (A) = n (número de incógnitas), el sistema es compatible determinado. Tiene una única solución, que se conoce con el nombre de solución trivial. Es aquella en la que todas las incógnitas son  nulas ( 0 ).

  2) Si rango (A) < n (número de incógnitas), el sistema es compatible indeterminado (tiene infinitas soluciones).

Una vez realizada la "discusión o identificación del sistema", aplicaremos alguno de los métodos que desarrollaremos en los epígrafes posteriores. No obstante, es preciso tener en cuenta las siguientes observaciones:

  1) Si el sistema es compatible determinado, el valor común de los rangos indica el número de ecuaciones principales, es decir, aquellas que no dependen de las restantes.

  2) Si el sistema es compatible indeterminado, (rango (A) = rango (A*) = k < n) el valor común de los rangos  ( k )  indica tanto el número de ecuaciones independientes o principales, como el número de incógnitas principales. Las restantes incógnitas  (no principales)  n - k  las pasaremos al segundo miembro formando un único término junto al término independiente. Siguiendo este procedimiento obtendremos un sistema de  k  ecuaciones lineales con  k incógnitas (principales), al que aplicaremos uno de los procedimientos que estudiaremos en los siguientes apartados: Regla de Cramer, Método de Gauss o, por la matriz inversa.

- Resolución de sistema homogéneos:

Sabemos que un sistema es homogéneo si todos los términos independientes son

cero, y que además, estos sistemas son siempre compatibles. Aplicando el Teorema de Rouché-Frobenius:

  1) Si Rang(A)= nº de incógnitas Î S.C.D. Solución trivial. (0,0,0).

  2) Si Rang(A)< nº de incógnitas Î S.C.I. Infinitas soluciones, entre ellas la (0,0,0).

Fuente: 

http://recursostic.educacion.es/descartes/web/materiales_didacticos/sistemas_de_ecuaciones_lineales_2bcnt/discusion_por_el_teorema_de_rouche.htm

http://www.vitutor.com/algebra/sistemas%20I/cramer.html

http://recursostic.educacion.es/descartes/web/materiales_didacticos/sistemas_de_ecuaciones_lineales_2bcnt/regla_de_cramer.htm

http://selectividad.intergranada.com/Matematicas/Clase/Tema_08-Teorema_Rouche.pdf

Mis apuntes