Si tenemos:
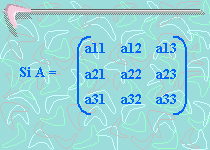



Veamos un ejemplo:
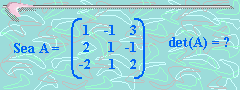
1. Vamos a resolverlo fijando la fila 1:

2. Ahora lo vamos a resolver fijando la fila 2:

3. Ahora lo vamos a resolver fijando la fila 3:
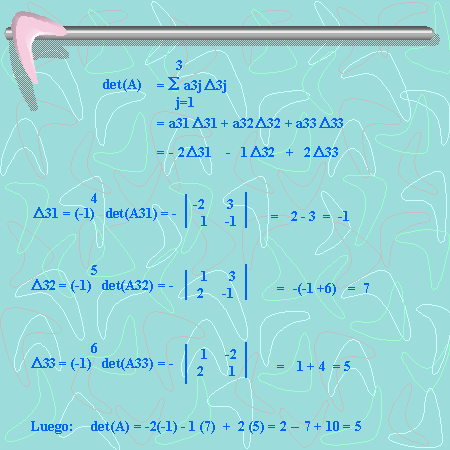
Como puedes ver, fijando la fila 1, 2 o 3 obtuvimos el mismo resultado. Ahora está en tí que te fijes cuál de las filas es la que te conviene tomar para resolver el ejercicio.
Veamos que pasa si lo resolvemos fijando las columnas.
4. Ahora lo vamos a resolver fijando la columna 1:
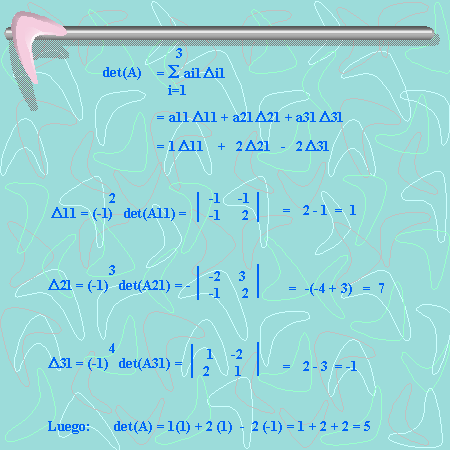
5. Resolvamos fijando la columna 2:

6. Finalmente lo vamos a resolver fijando la columna 3:
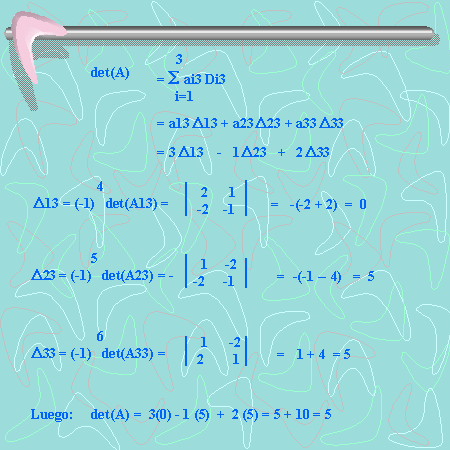
Al igual que en las filas, fijando la columna 1, 2 o 3 obtuvimos el mismo resultado. O sea , fijando cualquier fila o cualquier columna , obtendremos el mismo resultado. Pero usa tu ingenio para saber cual es más conveniente elegir.
- Método de Leibniz:
- Método de Leibniz:
En álgebra, la fórmula de Leibniz expresa el determinante de una matriz cuadrada:
En términos de permutaciones de los elementos de la matriz. Nombrado en honor de Gottfried Leibniz, la fórmula es:
Para una matriz n×n, donde sgn es la Función signo de Permutaciones en el grupo de la permutación Sn que devuelve +1 y -1 para permutaciones pares e impares, respectivamente.
Otra notación común usada para la fórmula es en términos del símbolo de Levi-Civita y hace uso de la notación de Einstein, donde se convierte:
que puede ser más familiar para los físicos.
Evaluar directamente la fórmula Leibniz de la definicion requiere  operaciones en generales decir un número de operaciones asintóticamente proporcionales a n factorial porque n! es el número n de ordenes de permutaciones. Esto es prácticamente difícil para grandes n. En su lugar, el determinante se puede evaluar en O(n)3 operaciones mediante la formación de la Descomposición LU]
operaciones en generales decir un número de operaciones asintóticamente proporcionales a n factorial porque n! es el número n de ordenes de permutaciones. Esto es prácticamente difícil para grandes n. En su lugar, el determinante se puede evaluar en O(n)3 operaciones mediante la formación de la Descomposición LU] 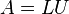 (normalmente a través de la Eliminación gaussiana o métodos similares), en cuyo caso
(normalmente a través de la Eliminación gaussiana o métodos similares), en cuyo caso  y los determinantes de las matrices triangulares L y U son simplemente los productos de sus entradas diagonales. (En los usos prácticos de álgebra lineal, sin embargo, raras vez requieren el cálculo explícito del determinante). Ver, por ejemplo, Trefethen y Bau (1997).
y los determinantes de las matrices triangulares L y U son simplemente los productos de sus entradas diagonales. (En los usos prácticos de álgebra lineal, sin embargo, raras vez requieren el cálculo explícito del determinante). Ver, por ejemplo, Trefethen y Bau (1997).
 operaciones en generales decir un número de operaciones asintóticamente proporcionales a n factorial porque n! es el número n de ordenes de permutaciones. Esto es prácticamente difícil para grandes n. En su lugar, el determinante se puede evaluar en O(n)3 operaciones mediante la formación de la Descomposición LU]
operaciones en generales decir un número de operaciones asintóticamente proporcionales a n factorial porque n! es el número n de ordenes de permutaciones. Esto es prácticamente difícil para grandes n. En su lugar, el determinante se puede evaluar en O(n)3 operaciones mediante la formación de la Descomposición LU] 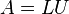 (normalmente a través de la Eliminación gaussiana o métodos similares), en cuyo caso
(normalmente a través de la Eliminación gaussiana o métodos similares), en cuyo caso  y los determinantes de las matrices triangulares L y U son simplemente los productos de sus entradas diagonales. (En los usos prácticos de álgebra lineal, sin embargo, raras vez requieren el cálculo explícito del determinante). Ver, por ejemplo, Trefethen y Bau (1997).
y los determinantes de las matrices triangulares L y U son simplemente los productos de sus entradas diagonales. (En los usos prácticos de álgebra lineal, sin embargo, raras vez requieren el cálculo explícito del determinante). Ver, por ejemplo, Trefethen y Bau (1997).
- Inversa de una matriz por determinantes:
Por definición de la matriz inversa sabemos que:  . Si calculamos el determinante de las dos partes de esta igualdad, y aplicamos las propiedades de los determinantes que ya conocemos , tenemos:
. Si calculamos el determinante de las dos partes de esta igualdad, y aplicamos las propiedades de los determinantes que ya conocemos , tenemos:
 . Si calculamos el determinante de las dos partes de esta igualdad, y aplicamos las propiedades de los determinantes que ya conocemos , tenemos:
. Si calculamos el determinante de las dos partes de esta igualdad, y aplicamos las propiedades de los determinantes que ya conocemos , tenemos:
Existe una propiedad recíproca de la primera de estas dos propiedades: si una matriz cuadrada tiene el determinante distinto de cero entonces tiene inversa.
No vamos a hacer una demostración completa sino que vamos a comprobar en un ejemplo que si el determinante de la matriz no es 0, podemos construir la matriz inversa. Para ello procedemos de la siguiente manera:
Consideremos la matriz  , cuyo determinante es 3. A partir de esta matriz vamos a construir una nueva matriz, que llamaremos la matriz adjunta de A, que está formada por los adjuntos de todos los elementos de A:
, cuyo determinante es 3. A partir de esta matriz vamos a construir una nueva matriz, que llamaremos la matriz adjunta de A, que está formada por los adjuntos de todos los elementos de A:
 , cuyo determinante es 3. A partir de esta matriz vamos a construir una nueva matriz, que llamaremos la matriz adjunta de A, que está formada por los adjuntos de todos los elementos de A:
, cuyo determinante es 3. A partir de esta matriz vamos a construir una nueva matriz, que llamaremos la matriz adjunta de A, que está formada por los adjuntos de todos los elementos de A:
Si ahora multiplicamos la matriz A por la traspuesta de su adjunta tenemos lo siguiente:
De donde deducimos que:  .
.
 .
.
Observa que esta construcción es posible si el determinante no es cero. En el anterior producto de las dos matrices se multiplican las filas de la matriz A por los adjuntos de una fila. Resulta que si multiplicamos una fila por la fila de sus adjuntos, sabemos que el resultado es el determinante de la matriz (es lo que ocurre en los elementos de la diagonal principal). También es fácil comprobar que si multiplicamos una fila por los adjuntos de otra fila el resultado es cero (en el resto de los elementos del producto) ya que es el desarrollo de una determinante en la que hay dos filas iguales.
- Rango:
El rango de una matriz es el número de filas (o columnas) linealmente independientes. Utilizando esta definición se puede calcular usando el método de Gauss.
1º Procedimiento: Calculamos un menor de orden 2. Si es distinto de 0, calculamos un menor de orden 3; en otro caso, calculamos un menor de orden 2. SI todos los menores de orden 2 son nulos, el rango de la matriz es un uno.
En caso contrario, si todos los menores de orden 3 son nulos, el rango es 2.
2º Procedimiento: Calculamos todos los determinantes del mayor orden posible, si hay alguno que no sea 0, el rango coincide con el orden de ese determinante. SI todos son cero, probamos con los menores de un orden inferior...
También podemos decir que el rango es: el orden de la mayor submatriz cuadrada no nula. Utilizando esta definición se puede calcular el rango usando determinantes.
- Tipo Vandermonde:
- Tipo Vandermonde:
Es una matriz que presenta una progresión geométrica en cada fila. Esta matriz recibe dicho nombre en honor al matemático francés Alexandre-Théophile Vandermonde.
Los índices de la matriz de tamaño n×n están descritos por  para todos los índices i y j variando de 1 a n, lo cual se puede describir explícitamente de la forma siguiente:
para todos los índices i y j variando de 1 a n, lo cual se puede describir explícitamente de la forma siguiente:
 para todos los índices i y j variando de 1 a n, lo cual se puede describir explícitamente de la forma siguiente:
para todos los índices i y j variando de 1 a n, lo cual se puede describir explícitamente de la forma siguiente:
En el primer elemento de cada fila hay solamente unos (al ser la potencia de cero) y en el segundo elemento hay una serie de números arbitrarios. En el tercero se encuentran esos mismos números elevados al cuadrado. En el cuarto están esos mismos números elevados al cubo y en las siguientes filas elevados a la potencia inmediatamente superior de manera que en el elemento n de cada fila esos números estén elevados a la potencia n-1.
Una matriz de Vandermonde es invertible si y sólo si todas las 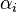 son distintas entre sí. Hay una fórmula para dicha inversa.
son distintas entre sí. Hay una fórmula para dicha inversa.
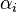 son distintas entre sí. Hay una fórmula para dicha inversa.
son distintas entre sí. Hay una fórmula para dicha inversa.
El determinante de una matriz de Vandermonde de tamaño n×n se expresa con la siguiente fórmula general:
Esta fórmula es denominada en algunas oportunidades como el discriminante, pero en general éste se define como el cuadrado de la fórmula anterior.
Esta fórmula se puede demostrar por inducción. Es fácil notar que en el caso de una matriz de 2×2 el resultado es correcto.
Ahora, generalizando para el caso n×n basta con realizar la siguiente operación elemental sobre cada columna  :
:  - (
- ( ×
×  ). Esta operación no afecta al determinante, por lo que se obtiene lo siguiente:
). Esta operación no afecta al determinante, por lo que se obtiene lo siguiente:
 :
:  - (
- ( ×
×  ). Esta operación no afecta al determinante, por lo que se obtiene lo siguiente:
). Esta operación no afecta al determinante, por lo que se obtiene lo siguiente:
Calculando el determinante, se elimina la primera fila de ceros y la primera columna de unos, quedando entonces el determinante de una matriz de n-1×n-1:
Siguiendo con el desarrollo de la determinante, se pueden factorizar los productos de diferencias ubicados en las diagonales quedando una nueva matriz de Vandermonde de n-1×n-1.
El proceso se puede repetir continuamente reduciendo el orden de la matriz, quedando así probado el procedimiento por inducción y la demostración de la fórmula indicada en un comienzo.
Fuente:
http://148.204.211.134/polilibros/portal/Polilibros/P_Terminados/Investigacion_de_Operaciones_Careaga/Common/IO-apendicea-matricesdetdeterminantes.htm
http://www.iesayala.com/selectividadmatematicas/ficheros/teoria/geometria/2_MATRICES.pdf
http://148.204.211.134/polilibros/portal/Polilibros/P_Terminados/Investigacion_de_Operaciones_Careaga/Common/IO-apendicea-matricesdetchio.htm
http://palillo.usach.cl/Pamela/
http://e-ducativa.catedu.es/44700165/aula/archivos/repositorio/4250/4346/html/23_clculo_de_la_inversa_con_determinantes.html
http://es.wikipedia.org/wiki/Matriz_de_Vandermonde
http://es.wikipedia.org/wiki/Fórmula_de_Leibniz_para_el_cálculo_de_determinantes







No hay comentarios:
Publicar un comentario