Matrices

Una matriz es un arreglo rectangular de mxn números, dispuestos en m filas y n columnas, generalmente encerrado en paréntesis.

Para cualquier m ó n y cualesquiera elementos a i j. Cada renglón y cada columna de la matriz A representan vectores, renglón y columna, respectivamente.

Matriz cuadrada.- Si m = n

Matriz diagonal.- Es una matriz cuadrada cuyos elementos fuera de la diagonal principal, los coeficientes a i j para i  j, son todos iguales a cero.

Matriz identidad ( I ).- Es una matriz diagonal cuyos coeficientes diagonales son 1.

Matriz traspuesta.- La traspuesta A^T de una matriz A es en la que los renglones y columnas se han intercambiado.

Matriz triangular.- Es una matriz cuadrada con los a i j = 0 para i > j ó los a i j = 0 para i < j.

Matriz simétrica.- Si una matriz cuadrada A = A^T ó a i j = a j i.

Matrices iguales.- Dos matrices son iguales si y solo si sus elementos correspondientes son iguales. Las dimensiones m x n también son iguales.

Matriz nula.- Si tiene todos sus elementos iguales a cero (0).

Orden de una matriz.- Es el número de renglones y columnas que tiene, así se dice una matriz de orden m X n ó de orden n si es cuadrada.

Suma de matrices.- Dadas las matrices A y B, ambas de orden m X n, la suma es una matriz C de orden m X n.

C = A  B = ( a i j )_mxn  ( b i j )_mxn = ( c i j )_mxn

Propiedades de la suma de matrices.

  1) Asociativa: A+(A+B)=(A+B)+C

  2) Conmutativa: A + B = B + A

  3) Existe elemento neutro: A + 0 = A

  4) Existe elemento opuesto: A+(-A)=0

  5) La transpuesta de la suma es igual a la suma de las transpuestas: (A+B)^t=A^t+B^t

       Ejemplo:

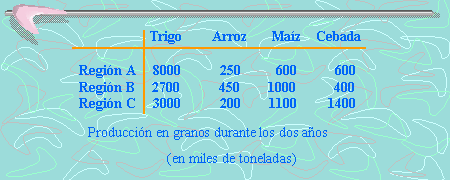
La siguiente información, corresponde a la producción en granos en miles de toneladas, en dos años consecutivos:

¿Cuál es la producción de granos en miles de toneladas durante los dos años consecutivos?

Para resolver este problema, debemos sumar la producción del primer año, con la producción del segundo año. Esto equivale a sumar los elementos de la primera matriz con los elementos correspondientes de la segunda matriz:

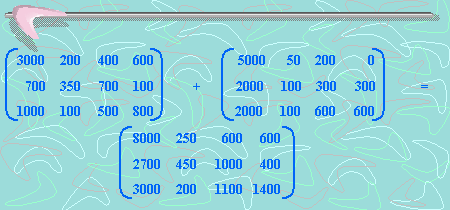
Lo que respondería nuestra pregunta.

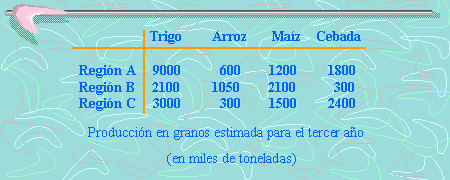
Supongamos ahora que existen muchos incentivos para incrementar la producción, condiciones climáticas favorables, etc. De tal forma que se estima que la producción para el tercer año será el triple de la producción del primero ¿Cuál será entonces, la producción estimada de este último año?

En este caso, debemos multiplicar la producción del primer año por tres (recuerda que es el triple).

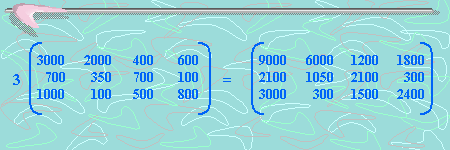
Luego tenemos:

Para solucionar los problemas anteriores, acabamos de utilizar dos operaciones muy importantes con matrices: la suma y la multiplicación por un escalar (un número Real).

La suma de dos matrices, sean A =(aij) y B = (bij), solo es posible cuando ambas matrices tienen la misma dimensión u orden. Esto es,  sean A = (aij)  y  B = (bij) matrices de orden (nxm) con elementos pertenecientes a los números reales.

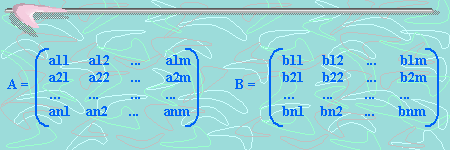
Si sumamos A + B obtendremos una matriz C = (cij) con elementos también pertenecientes a los números reales y del   mismo orden:

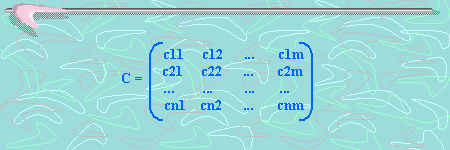
Donde los elementos de la matriz C son de la forma:

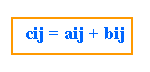
Veamos un ejemplo:

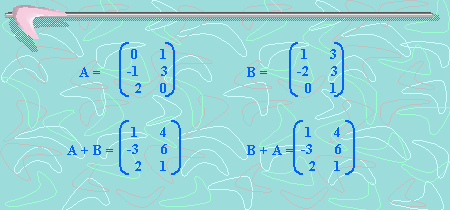
Tenemos que A + B  = B + A ¿Será conmutativa la suma de matrices?

Por supuesto que es conmutativa, puedes ver la demostración: CLICK AQUI

Ahora si que podemos afirmar que la suma de matrices es conmutativa. O sea:

 

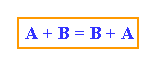
Consideremos lo siguiente:

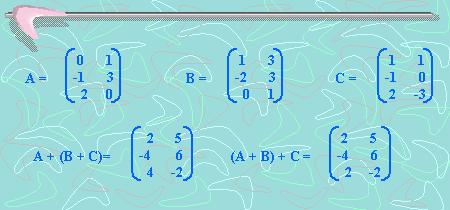
Multiplicación de una matriz por un escalar.- Dado un escalar , - <  < , y una matriz A m x n

B =   =  (a i j) = ( a i j) = (b i j)

Propiedades de la multiplicación por un escalar.

Multiplicación de matrices.- El producto AB de dos matrices está definido sólo en caso de que el número de columnas de A sea igual al número de renglones de B. El producto AB no es conmutativo, o sea A B  B A.

Cuando se cumple con la condición mencionada (n_A = m_B) se dice que ambas matrices son conformables para el producto.

Propiedades de la multiplicación de matrices.

Ejemplos:

La siguiente información corresponde a la cantidad de vitaminas A, B y C contenidas en cada unidad de los alimentos I y II.

 

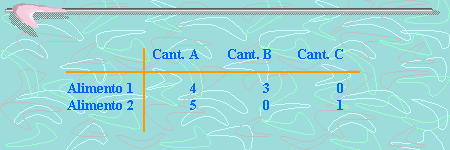
Si ingerimos cinco unidades del alimento I y dos unidades del alimento II ¿Cuánto consumiremos de cada tipo de vitamina?

Para resolver este problema, representemos el consumo de los alimentos I y II (en este orden) en la siguiente matriz:

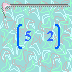
La operación que nos va a permitir obtener la cantidad ingerida de cada vitamina es la siguiente:

 

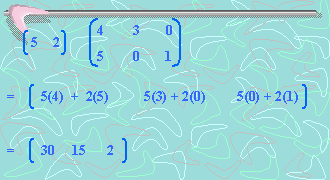
Esto quiere decir que serán ingeridas 30 unidades de vitamina A, 15 unidades de vitamina B y 2 unidades de vitamina C. Lo que respondería nuestra interrogante.

Supongamos ahora que el costo de los alimentos depende solamente de su contenido vitamínico y sabemos que los precios por unidad de vitamina A, B y C son respectivamente $5, $3 y $5. Entonces ¿Cuánto pagaremos por la porción de alimentos indicada anteriormente?

Esto lo podemos resolver de la siguiente forma:

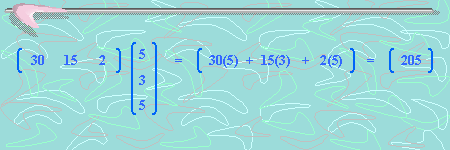
Esto quiere decir que pagaríamos $205.

Propiedades de las matrices traspuestas.

• (A^T)^T = A
• (A + B)^T = A^T + B^T
• (A + B + ... +N)^T = A^T + B^T + ... + N^T
• (AB)^T = B^T A^T
• (A B...N)^T = N^T ... B^T A^T
• A^TB = B^TA
  
  Fuente:
  http://148.204.211.134/polilibros/portal/Polilibros/P_Terminados/Investigacion_de_Operaciones_Careaga/Common/IO-apendicea-matricesdet.htm
  http://palillo.usach.cl/Pamela/suma.htm
  http://palillo.usach.cl/Pamela/mult.htm
  Mis apuntes