El objetivo de este apartado es examinar los aspectos numéricos que se presentan al resolver sistemas de ecuaciones lineales de la forma:
Se trata de un sistema de n ecuaciones con n incógnitas, x1, x2, ..., xn. Los elementos aij y bi son números reales fijados.
El sistema de ecuaciones se puede escribir, empleando una muy útil representación matricial, como:
Entonces podemos denotar estas matrices por A, x y b de forma que la ecuación se reduce simplemente a:
| Ax=b |
Los métodos de resolución de sistemas de ecuaciones se pueden dividir en dos grandes grupos:
- Los Métodos exactos o algoritmos finitos que permiten obtener la solución del sistema de manera directa.
- Los Métodos aproximados que utilizan algoritmos iterativos e infinitos y que calculan las solución del sistema por aproximaciones sucesivas.
De entre los métodos exactos analizaremos el método de Gauss y una modificación de éste denominado método de Gauss-Jordan. Entre los métodos aproximados nos centraremos en el estudio de los métodos de Richardson, Jacobi y Gauss-Seidel.
- Método de eliminación para resolver sistemas de ecuaciones lineales de Gauss - Jordan:
Para resolver un sistema de ecuaciones con este método se emplea la eliminación sucesiva de las incógnitas según este esquema: Considere las siguientes m ecuaciones lineales:
Ahora se arregla una matriz B de este sistema, ampliada con los bi (línea vertical).
Después se hacen transformaciones elementales con los renglones de la matriz, lo cual es equivalente a hacerlo con las respectivas ecuaciones:
- Se permite cambiar el orden de las filas.
- Se pueden multiplicar los renglones por cualquier número diferente de cero.
- Sumar a un renglón de la matriz, otra fila multiplicada por cualquier número.
Así se obtiene una matriz ampliada de un nuevo sistema equivalente al original pues se reduce la matriz B a la forma más sensilla posible que incluya la solución del sistema. A continuación se presenta el procedimiento detallado:
- Intercambio de ecuaciones y de la posición de las incógnitas para que a11
 0.
0. - Multiplicación de la primera ecuación por una constante apropiada diferente de cero, para lograr a11 = 1.
- Para toda i > 1, se multiplica la primera ecuación por -ai1 y luego se suma a la i-ésima ecuación, de tal manera que la primera incógnita queda eliminada.
Considere el siguiente ejemplo con anotaciones del cálculo a la izquierda:
La matriz ampliada de este sistema es:
Se resta: el renglón (1) del (2) y el (3), el (1)(3) al (4), resultando la matriz:
Se permutan los renglones (2) y (3) para tener el coeficiente 1en renglón 2
El renglón (2) se duplica y se resta al (1) y al (4), el (2) se triplica y se resta al (3)
El (3) se divide entre (-14), el coeficiente 1 resultante se usa para operar con el cálculo que se indica en la columna izquierda
La columna derecha de la última matriz tiene la solución del sistema propuesto: X1 = -1, X2 = 0, X3 = 1
Ecuacion lineal degenerativa.- Así llamada cuando todos los coeficientes de las incógnitas son cero. En el caso especial de un sistema en que todas las ecuaciones son degenerativas ( aij = 0), se tienen dos casos:
aij = 0), se tienen dos casos:
 aij = 0), se tienen dos casos:
aij = 0), se tienen dos casos:- El sistema tiene por lo menos una ecuación de la forma: 0x1 + 0x2 +...+ 0xn = bi con bi
 0, entonces esta ecuación y por lo tanto el sistema, no tiene solución, (es inconsistente).
0, entonces esta ecuación y por lo tanto el sistema, no tiene solución, (es inconsistente). - Todas las ecuaciones del sistema son de la forma: 0x1 + 0x2 +...+ 0xn = 0, entonces cada ecuación y, por lo tanto el sistema tienen toda "n-ada" de números reales como solución.
En el caso común cuando las ecuaciones no son todas degenerativas (aij  0), el sistema de ecuaciones se reduce a uno más simple equivalente al original que posee las mismas soluciones, el proceso se lleva hasta eliminación completa (Gauss-Jordan) para obtener la solución.
0), el sistema de ecuaciones se reduce a uno más simple equivalente al original que posee las mismas soluciones, el proceso se lleva hasta eliminación completa (Gauss-Jordan) para obtener la solución.
 0), el sistema de ecuaciones se reduce a uno más simple equivalente al original que posee las mismas soluciones, el proceso se lleva hasta eliminación completa (Gauss-Jordan) para obtener la solución.
0), el sistema de ecuaciones se reduce a uno más simple equivalente al original que posee las mismas soluciones, el proceso se lleva hasta eliminación completa (Gauss-Jordan) para obtener la solución.
Si se encuentra una ecuación de la forma 0x1 +... +0xn = 0 puede quitarse sin que afecte la solución.
Continuando con el proceso anterior, con cada nuevo subsistema, se obtiene por inducción, que el sistema o bién no tiene solución, ó bien es reductible a una forma equivalente.
Para la solución de un sistema de ecuaciones lineales en forma escalonada (eliminación de Gauss-Jordan), hay dos casos:
- Si hay tantas ecuaciones como incógnitas (m-=n) entonces el sistema tiene una solución única.
- Si hay menos ecuaciones que incógnitas (m < m + n) entonces se pueden asignar arbitrariamente valores a las n variables llamadas en este caso "libres" y obtener una solución del sistema. Si se asignan valores diferentes a tales "variables libres", se pueden obtener muchas soluciones del sistema.
Para el caso particular de un sistema homogéneo de ecuaciones lineales reducido a la forma escalonada se presentan dos posibilidades.
1)Tantas ecuaciones como incógnitas (m = n), entonces la solución es (0, 0,.....0) ó trivial.
2) Menos ecuaciones que incógnitas (m < m + n), entonces el sistema tiene una solución no nula. En resumen:
- Método de Richardson:
El método de Richardson toma como matriz Q la matriz identidad (I). En este caso la ecuación queda en la forma:| Ix(k) = (I-A)x(k-1)+b = x(k-1)+r(k-1) |
en donde r(k-1) es el vector residual definido mediante r(k-1)=b-Ax(k-1).La matriz identidad es aquella matriz diagonal cuyos elementos no nulos son 1, es decir:

y cumple que
IA = A
para cualquier valor de A; es decir, es el elemento neutro del producto matricial. De acuerdo con esto, la ecuación se puede escribir como:
x(k) = x(k-1) - Ax(k-1) + b = x(k-1) + r(k-1)
en donde un elemento cualquiera del vector r(k-1) vendrá dado por la expresión:

En la siguiente figura se muestra un algoritmo para ejecutar la iteración de Richardson. Este método recibe también el nombre de método de relajación o método de los residuos.
- Método de Jacobi:
En la iteración de Jacobi, se escoge una matriz Q que es diagonal y cuyos elementos diagonales son los mismos que los de la matriz A. La matriz Q toma la forma:
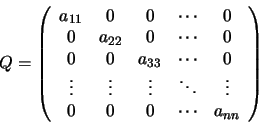
y la ecuación general se puede escribir como
Si denominamos R a la matriz A-Q:

la ecuación anterior se puede reescribir como:
El producto de la matriz Q por el vector columna x(k) será un vector columna. De modo análogo, el producto de la matriz R por el vector columna x(k-1) será también un vector columna. La expresión anterior, que es una ecuación vectorial, se puede expresar por necuaciones escalares (una para cada componente del vector). De este modo, podemos escribir, para un elemento i cualquiera y teniendo en cuenta que se trata de un producto matriz-vector:
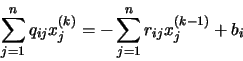
Si tenemos en cuenta que en la matriz Q todos los elementos fuera de la diagonal son cero, en el primer miembro el único término no nulo del sumatorio es el que contiene el elemento diagonal qii, que es precisamente aii. Más aún, los elementos de la diagonal de Rson cero, por lo que podemos eliminar el término i=j en el sumatorio del segundo miembro. De acuerdo con lo dicho, la expresión anterior se puede reescribir como:
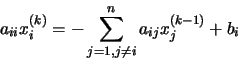
de donde despejando xi(k) obtenemos:
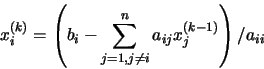
que es la expresión que nos proporciona las nuevas componentes del vector x(k) en función de vector anterior x(k-1) en la iteración de Jacobi. En la figura siguiente se presenta un algoritmo para el método de Jacobi.
El método de Jacobi se basa en escribir el sistema de ecuaciones en la forma:
Partimos de una aproximación inicial para las soluciones al sistema de ecuaciones y sustituimos estos valores en la ecuación anterior. De esta forma, se genera una nueva aproximación a la solución del sistema, que en determinadas condiciones, es mejor que la aproximación inicial. Esta nueva aproximación se puede sustituir de nuevo en la parte derecha de la ecuación anterior y así sucesivamente hasta obtener la convergencia.
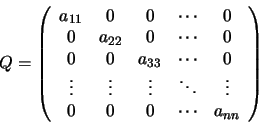
y la ecuación general se puede escribir como
| Qx(k) = (Q-A)x(k-1) + b |
Si denominamos R a la matriz A-Q:

la ecuación anterior se puede reescribir como:
Qx(k) = -Rx(k-1) + b
El producto de la matriz Q por el vector columna x(k) será un vector columna. De modo análogo, el producto de la matriz R por el vector columna x(k-1) será también un vector columna. La expresión anterior, que es una ecuación vectorial, se puede expresar por necuaciones escalares (una para cada componente del vector). De este modo, podemos escribir, para un elemento i cualquiera y teniendo en cuenta que se trata de un producto matriz-vector:
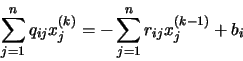
Si tenemos en cuenta que en la matriz Q todos los elementos fuera de la diagonal son cero, en el primer miembro el único término no nulo del sumatorio es el que contiene el elemento diagonal qii, que es precisamente aii. Más aún, los elementos de la diagonal de Rson cero, por lo que podemos eliminar el término i=j en el sumatorio del segundo miembro. De acuerdo con lo dicho, la expresión anterior se puede reescribir como:
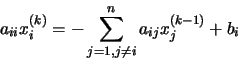
de donde despejando xi(k) obtenemos:
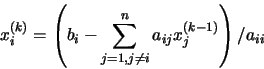
que es la expresión que nos proporciona las nuevas componentes del vector x(k) en función de vector anterior x(k-1) en la iteración de Jacobi. En la figura siguiente se presenta un algoritmo para el método de Jacobi.
El método de Jacobi se basa en escribir el sistema de ecuaciones en la forma:
Partimos de una aproximación inicial para las soluciones al sistema de ecuaciones y sustituimos estos valores en la ecuación anterior. De esta forma, se genera una nueva aproximación a la solución del sistema, que en determinadas condiciones, es mejor que la aproximación inicial. Esta nueva aproximación se puede sustituir de nuevo en la parte derecha de la ecuación anterior y así sucesivamente hasta obtener la convergencia.
- Método de Gauss-Seidel:
La iteración de Gauss-Seidel se define al tomar Q como la parte triangular inferior de A incluyendo los elementos de la diagonal: 
Si, como en el caso anterior, definimos la matriz R=A-Q

y la ecuación se puede escribir en la forma:
Qx(k) = -Rx(k-1) + b
Un elemento cualquiera, i, del vector Qx(k) vendrá dado por la ecuación:
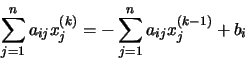
Si tenemos en cuenta la peculiar forma de las matrices Q y R, resulta que todos los sumandos para los que j > i en la parte izquierda son nulos, mientras que en la parte derecha son nulos todos los sumandos para los que
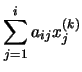 | = | 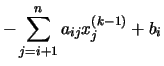 | |
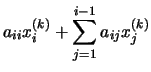 | = | 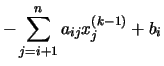 |
de donde despejando xi(k), obtenemos:
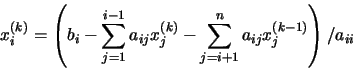
Obsérvese que en el método de Gauss-Seidel los valores actualizados de xi sustituyen de inmediato a los valores anteriores, mientras que en el método de Jacobi todas las componentes nuevas del vector se calculan antes de llevar a cabo la sustitución. Por contra, en el método de Gauss-Seidel los cálculos deben llevarse a cabo por orden, ya que el nuevo valor xi depende de los valores actualizados de x1, x2, ..., xi-1.
En la figura siguiente se incluye un algoritmo para la iteración de Gauss-Seidel.
Fuente:
http://148.204.211.134/polilibros/portal/Polilibros/P_Terminados/Investigacion_de_Operaciones_Careaga/Common/IO-apendicea-eqlinealesgaussjordan.htm
http://www.uv.es/~diaz/mn/node25.html
http://www.uv.es/~diaz/mn/node34.html
http://www.uv.es/~diaz/mn/node35.html
http://www.uv.es/~diaz/mn/node36.html












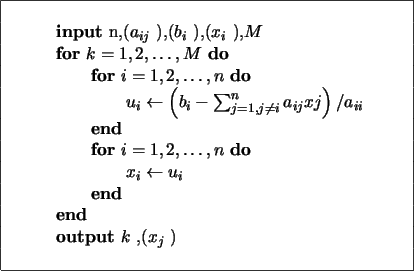
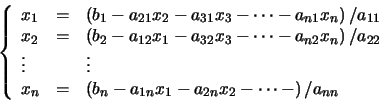
No hay comentarios:
Publicar un comentario