La teoría de grafos es muy importante en la actualidad: su utilización en redes, comunicación, biología o sociología hacen de esta rama de las matemáticas una herramienta esencial para el estudio y la modelización de muchos aspectos de nuestra vida.
Para las matemáticas y las ciencias de la computación, un grafo es el principal objeto de estudio de la teoría de grafos. De esta forma, un grafo se representa gráficamente como un conjunto de puntos (llamados vértices o nodos), unidos por líneas (aristas). Los grafos permiten estudiar las interrelaciones entre unidades que se encuentran en interacción.
Son diagramas que si se interpretan en forma adecuada proporcionan información, como por ejemplo los mapas, diagramas de circuitos o de flujos, entre otros
.
- Historia:
El origen de la teoría de grafos se remonta al siglo XVIII con el problema de los puentes de Königsberg, el cual consistía en encontrar un camino que recorriera los siete puentes del río Pregel (54°42′12″N 20°30′56″E) en la ciudad de Königsberg, actualmente Kaliningrado, de modo que se recorrieran todos los puentes pasando una sola vez por cada uno de ellos. El trabajo de Leonhard Euler sobre el problema titulado Solutio problematis ad geometriam situs pertinentis1 (La solución de un problema relativo a la geometría de la posición) en 1736, es considerado el primer resultado de la teoría de grafos. También se considera uno de los primeros resultados topológicos en geometría (que no depende de ninguna medida). Este ejemplo ilustra la profunda relación entre la teoría de grafos y la topología.
Luego, en 1847, Gustav Kirchhoff utilizó la teoría de grafos para el análisis de redes eléctricas publicando sus leyes de los circuitos para calcular el voltaje y la corriente en los circuitos eléctricos, conocidas como leyes de Kirchhoff, considerado la primera aplicación de la teoría de grafos a un problema de ingeniería.
En 1852 Francis Guthrie planteó el problema de los cuatro colores el cual afirma que es posible, utilizando solamente cuatro colores, colorear cualquier mapa de países de tal forma que dos países vecinos nunca tengan el mismo color. Este problema, que no fue resuelto hasta un siglo después por Kenneth Appel y Wolfgang Haken en 1976, puede ser considerado como el nacimiento de la teoría de grafos. Al tratar de resolverlo, los matemáticos definieron términos y conceptos teóricos fundamentales de los grafos.
En 1857, Arthur Cayley estudió y resolvió el problema de enumeración de los isómeros, compuestos químicos con idéntica composición (formula) pero diferente estructura molecular. Para ello represento cada compuesto, en este caso hidrocarburos saturados CnH2n+2, mediante un grafo árbol donde los vértices representan átomos y las aristas la existencia de enlaces químicos.
El término «grafo», proviene de la expresión «graphic notation» usada por primera vez por Edward Frankland2 y posteriormente adoptada por Alexander Crum Brown en 1884, y hacía referencia a la representación gráfica de los enlaces entre los átomos de una molécula.
El primer libro sobre teoria de grafos fue escrito por Dénes Kőnig y publicado en 1936.
- Aplicaciones:
Gracias a la teoría de grafos se pueden resolver diversos problemas como por ejemplo la síntesis de circuitos secuenciales, contadores o sistemas de apertura. Se utiliza para diferentes áreas por ejemplo, Dibujo computacional, en toda las áreas de Ingeniería.
Los grafos se utilizan también para modelar trayectos como el de una línea de autobús a través de las calles de una ciudad, en el que podemos obtener caminos óptimos para el trayecto aplicando diversos algoritmos como puede ser el algoritmo de Floyd.
Para la administración de proyectos, utilizamos técnicas como PERT en las que se modelan los mismos utilizando grafos y optimizando los tiempos para concretar los mismos.
La teoría de grafos también ha servido de inspiración para las ciencias sociales, en especial para desarrollar un concepto no metafórico de red social que sustituye los nodos por los actores sociales y verifica la posición, centralidad e importancia de cada actor dentro de la red. Esta medida permite cuantificar y abstraer relaciones complejas, de manera que la estructura social puede representarse gráficamente. Por ejemplo, una red social puede representar la estructura de poder dentro de una sociedad al identificar los vínculos (aristas), su dirección e intensidad y da idea de la manera en que el poder se transmite y a quiénes.
Los grafos son importantes en el estudio de la biología y hábitat. El vértice representa un hábitat y las aristas (o "edges" en inglés) representa los senderos de los animales o las migraciones. Con esta información, los científicos pueden entender cómo esto puede cambiar o afectar a las especies en su hábitat.
- Composición:
Un grafo está compuesto por dos conjuntos finitos, un conjunto de |A| aristas y un conjunto de |V| vértices. J es la relación de incidencia, que asocia a cada elemento de |A| un par de elementos de |V|
Se denota G= { A, V, j}
* Vértices: Son los objetos representados por punto dentro del grafo.
* Aristas Adyacentes: dos aristas son adyacentes si convergen sobre el mismo vértice.
* Aristas Múltiples o Paralelas: dos aristas son múltiples o paralelas si tienen los mismos vértices en común o incidente sobre los mismos vértices.
* Lazo: es una arista cuyos extremos inciden sobre el mismo vértice.
- Tipos de grafos:
* No dirigidos: son aquellos en los cuales los lados no están orientados (no son flechas). Cada lado se representa entre paréntesis, separando sus vértices por comas, y teniendo en cuenta (vi,vj)=(vj,vi).
* Dirigidos: son aquellos en los cuales los lados están orientados (flechas). Cada lado se representa entre ángulos, separando sus vértices por comas y teniendo en cuenta <vi ,vj>=<Vj ,vi>. En grafos dirigidos, para cada lado <a,b>, a, el cual es el vértice origen, se conoce como la cola del lado y b, el cual es el vértice destino, se conoce como cabeza del lado.
* Grafo simple. o simplemente grafo es aquel que acepta una sola una arista uniendo dos vértices cualesquiera. Esto es equivalente a decir que una arista cualquiera es la única que une dos vértices específicos. Es la definición estándar de un grafo.
* Grafo etiquetado. Grafos en los cuales se ha añadido un peso a las aristas (número entero generalmente) o un etiquetado a los vértices.
* Grafo aleatorio. Grafo cuyas aristas están asociadas a una probabilidad.
Hipergrafo. Grafos en los cuales las aristas tienen más de dos extremos, es decir, las aristas son incidentes a 3 o más vértices.
* Grafo infinito. Grafos con conjunto de vértices y aristas de cardinal infinito.
- Representación de grafos:
Existen diferentes formas de representar un grafo (simple), además de la geométrica y muchos métodos para almacenarlos en una computadora. La estructura de datos usada depende de las características del grafo y el algoritmo usado para manipularlo. Entre las estructuras más sencillas y usadas se encuentran las listas y las matrices, aunque frecuentemente se usa una combinación de ambas. Las listas son preferidas en grafos dispersos porque tienen un eficiente uso de la memoria. Por otro lado, las matrices proveen acceso rápido, pero pueden consumir grandes cantidades de memoria.
* Estructura de lista
- Lista de incidencia - Las aristas son representadas con un vector de pares (ordenados, si el grafo es dirigido), donde cada par representa una de las aristas.
- Lista de adyacencia - Cada vértice tiene una lista de vértices los cuales son adyacentes a él. Esto causa redundancia en un grafo no dirigido (ya que A existe en la lista de adyacencia de B y viceversa), pero las búsquedas son más rápidas, al costo de almacenamiento extra.
- Lista de grados - También llamada secuencia de grados o sucesión gráfica de un grafo no-dirigido es una secuencia de números, que corresponde a los grados de los vértices del grafo.
* Estructuras matriciales:
- Matriz de adyacencia - El grafo está representado por una matriz cuadrada M de tamaño n^2, donde n es el número de vértices. Si hay una arista entre un vértice x y un vértice y, entonces el elemento m_{x, y} es 1, de lo contrario, es 0.
- Matriz de incidencia - El grafo está representado por una matriz de A (aristas) por V (vértices), donde [arista, vértice] contiene la información de la arista (1 - conectado, 0 - no conectado)
- Ciclos y caminos:
Un ciclo es una sucesión de aristas adyacentes, donde no se recorre dos veces la misma arista, y donde se regresa al punto inicial.
Un ciclo hamiltoniano tiene además que recorrer todos los vértices exactamente una vez (excepto el vértice del que parte y al cual llega).
Por ejemplo, en un museo grande (al estilo del Louvre), lo idóneo sería recorrer todas las salas una sola vez, esto es buscar un ciclo hamiltoniano en el grafo que representa el museo (los vértices son las salas, y las aristas los corredores o puertas entre ellas).
Se habla también de camino Hamiltoniano si no se impone regresar al punto de partida, como en un museo con una única puerta de entrada. Por ejemplo, un caballo puede recorrer todas las casillas de un tablero de ajedrez sin pasar dos veces por la misma: es un camino hamiltoniano. Ejemplo de un ciclo hamiltoniano en el grafo del dodecaedro.
- Grafos planos:
Cuando un grafo o multigrafo se puede dibujar en un plano sin que dos segmentos se corten, se dice que es plano.
Un juego muy conocido es el siguiente: Se dibujan tres casas y tres pozos. Todos los vecinos de las casas tienen el derecho de utilizar los tres pozos. Como no se llevan bien en absoluto, no quieren cruzarse jamás. ¿Es posible trazar los nueve caminos que juntan las tres casas con los tres pozos sin que haya cruces?
Cualquier disposición de las casas, los pozos y los caminos implica la presencia de al menos un cruce.
Sea Kn el grafo completo con n vértices, Kn, p es el grafo bipartito de n y p vértices.
El juego anterior equivale a descubrir si el grafo bipartito completo K3,3 es plano, es decir, si se puede dibujar en un plano sin que haya cruces, siendo la respuesta que no. En general, puede determinarse que un grafo no es plano, si en su diseño puede encontrase una estructura análoga (conocida como menor) a K5 o a K3,3.
Establecer qué grafos son planos no es obvio, y es un problema que tiene que ver con topología.
Fuentes:




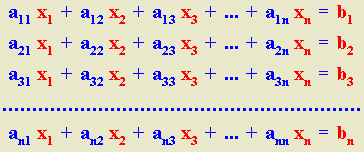





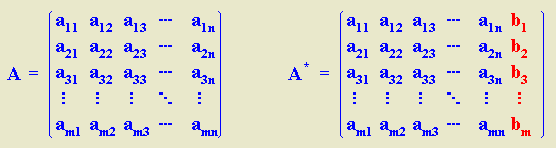




 0.
0.





 aij = 0), se tienen dos casos:
aij = 0), se tienen dos casos:



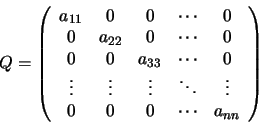

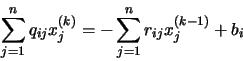
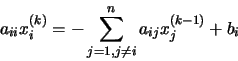
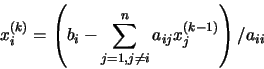
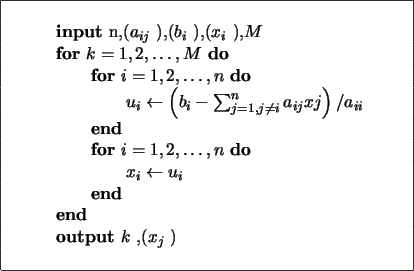
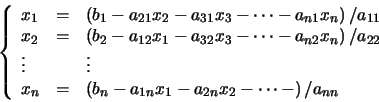


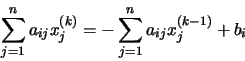
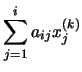
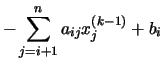
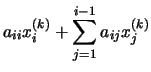
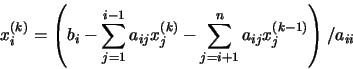
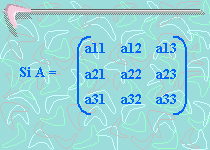





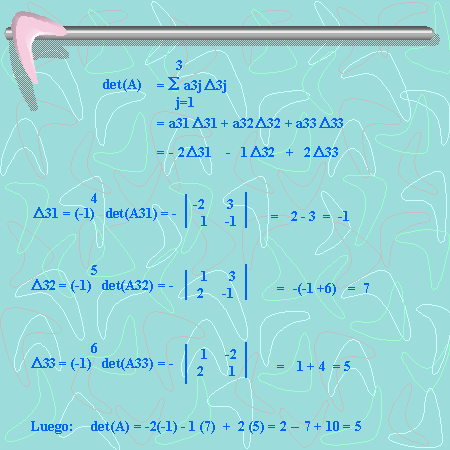
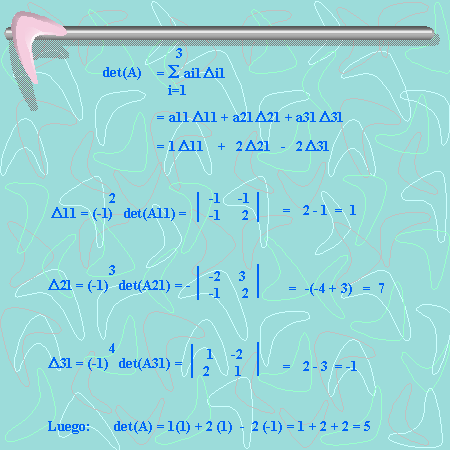

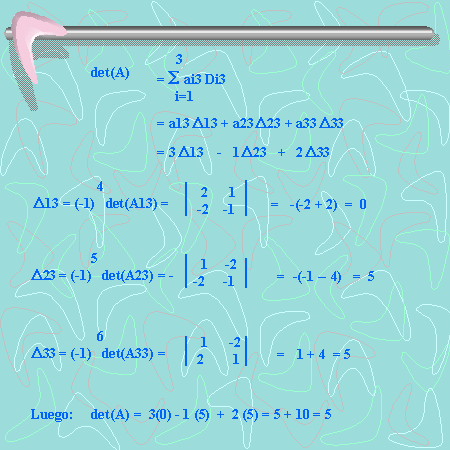



 operaciones en generales decir un número de operaciones asintóticamente proporcionales a n factorial porque n! es el número n de ordenes de permutaciones. Esto es prácticamente difícil para grandes n. En su lugar, el determinante se puede evaluar en O(n)3 operaciones mediante la formación de la Descomposición LU]
operaciones en generales decir un número de operaciones asintóticamente proporcionales a n factorial porque n! es el número n de ordenes de permutaciones. Esto es prácticamente difícil para grandes n. En su lugar, el determinante se puede evaluar en O(n)3 operaciones mediante la formación de la Descomposición LU] 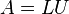 (normalmente a través de la Eliminación gaussiana o métodos similares), en cuyo caso
(normalmente a través de la Eliminación gaussiana o métodos similares), en cuyo caso  y los determinantes de las matrices triangulares L y U son simplemente los productos de sus entradas diagonales. (En los usos prácticos de álgebra lineal, sin embargo, raras vez requieren el cálculo explícito del determinante). Ver, por ejemplo, Trefethen y Bau (1997).
y los determinantes de las matrices triangulares L y U son simplemente los productos de sus entradas diagonales. (En los usos prácticos de álgebra lineal, sin embargo, raras vez requieren el cálculo explícito del determinante). Ver, por ejemplo, Trefethen y Bau (1997). . Si calculamos el determinante de las dos partes de esta igualdad, y aplicamos las propiedades de los determinantes que ya conocemos , tenemos:
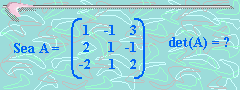
. Si calculamos el determinante de las dos partes de esta igualdad, y aplicamos las propiedades de los determinantes que ya conocemos , tenemos: , cuyo determinante es 3. A partir de esta matriz vamos a construir una nueva matriz, que llamaremos la matriz adjunta de A, que está formada por los adjuntos de todos los elementos de A:
, cuyo determinante es 3. A partir de esta matriz vamos a construir una nueva matriz, que llamaremos la matriz adjunta de A, que está formada por los adjuntos de todos los elementos de A:
 .
. para todos los índices i y j variando de 1 a n, lo cual se puede describir explícitamente de la forma siguiente:
para todos los índices i y j variando de 1 a n, lo cual se puede describir explícitamente de la forma siguiente:
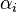 son distintas entre sí. Hay una fórmula para dicha inversa.
son distintas entre sí. Hay una fórmula para dicha inversa. :
:  ×
×  ). Esta operación no afecta al determinante, por lo que se obtiene lo siguiente:
). Esta operación no afecta al determinante, por lo que se obtiene lo siguiente:

