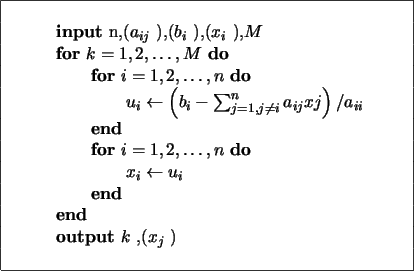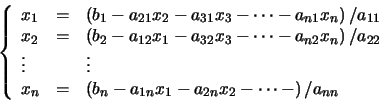Éste es el segundo examen, el cual lo volví a hacer en casa, y lo quiero presentar como repaso para subir nota en el examen global de la 2ª evaluación:
El país de las matemáticas
sábado, 1 de febrero de 2014
Ejercicios de vectores
Estos ejercicios los he hecho para subir nota en el primer examen de la 2º evaluación.
Los enunciados corresponden a la hoja que colgaste de ejercicios sobre vectores para el repaso del primer examen.
lunes, 11 de noviembre de 2013
Teoría de grafos
La teoría de grafos es muy importante en la actualidad: su utilización en redes, comunicación, biología o sociología hacen de esta rama de las matemáticas una herramienta esencial para el estudio y la modelización de muchos aspectos de nuestra vida.
Para las matemáticas y las ciencias de la computación, un grafo es el principal objeto de estudio de la teoría de grafos. De esta forma, un grafo se representa gráficamente como un conjunto de puntos (llamados vértices o nodos), unidos por líneas (aristas). Los grafos permiten estudiar las interrelaciones entre unidades que se encuentran en interacción.
Son diagramas que si se interpretan en forma adecuada proporcionan información, como por ejemplo los mapas, diagramas de circuitos o de flujos, entre otros
.
- Historia:
El origen de la teoría de grafos se remonta al siglo XVIII con el problema de los puentes de Königsberg, el cual consistía en encontrar un camino que recorriera los siete puentes del río Pregel (54°42′12″N 20°30′56″E) en la ciudad de Königsberg, actualmente Kaliningrado, de modo que se recorrieran todos los puentes pasando una sola vez por cada uno de ellos. El trabajo de Leonhard Euler sobre el problema titulado Solutio problematis ad geometriam situs pertinentis1 (La solución de un problema relativo a la geometría de la posición) en 1736, es considerado el primer resultado de la teoría de grafos. También se considera uno de los primeros resultados topológicos en geometría (que no depende de ninguna medida). Este ejemplo ilustra la profunda relación entre la teoría de grafos y la topología.
Luego, en 1847, Gustav Kirchhoff utilizó la teoría de grafos para el análisis de redes eléctricas publicando sus leyes de los circuitos para calcular el voltaje y la corriente en los circuitos eléctricos, conocidas como leyes de Kirchhoff, considerado la primera aplicación de la teoría de grafos a un problema de ingeniería.
En 1852 Francis Guthrie planteó el problema de los cuatro colores el cual afirma que es posible, utilizando solamente cuatro colores, colorear cualquier mapa de países de tal forma que dos países vecinos nunca tengan el mismo color. Este problema, que no fue resuelto hasta un siglo después por Kenneth Appel y Wolfgang Haken en 1976, puede ser considerado como el nacimiento de la teoría de grafos. Al tratar de resolverlo, los matemáticos definieron términos y conceptos teóricos fundamentales de los grafos.
En 1857, Arthur Cayley estudió y resolvió el problema de enumeración de los isómeros, compuestos químicos con idéntica composición (formula) pero diferente estructura molecular. Para ello represento cada compuesto, en este caso hidrocarburos saturados CnH2n+2, mediante un grafo árbol donde los vértices representan átomos y las aristas la existencia de enlaces químicos.
El término «grafo», proviene de la expresión «graphic notation» usada por primera vez por Edward Frankland2 y posteriormente adoptada por Alexander Crum Brown en 1884, y hacía referencia a la representación gráfica de los enlaces entre los átomos de una molécula.
El primer libro sobre teoria de grafos fue escrito por Dénes Kőnig y publicado en 1936.
- Aplicaciones:
Gracias a la teoría de grafos se pueden resolver diversos problemas como por ejemplo la síntesis de circuitos secuenciales, contadores o sistemas de apertura. Se utiliza para diferentes áreas por ejemplo, Dibujo computacional, en toda las áreas de Ingeniería.
Los grafos se utilizan también para modelar trayectos como el de una línea de autobús a través de las calles de una ciudad, en el que podemos obtener caminos óptimos para el trayecto aplicando diversos algoritmos como puede ser el algoritmo de Floyd.
Para la administración de proyectos, utilizamos técnicas como PERT en las que se modelan los mismos utilizando grafos y optimizando los tiempos para concretar los mismos.
La teoría de grafos también ha servido de inspiración para las ciencias sociales, en especial para desarrollar un concepto no metafórico de red social que sustituye los nodos por los actores sociales y verifica la posición, centralidad e importancia de cada actor dentro de la red. Esta medida permite cuantificar y abstraer relaciones complejas, de manera que la estructura social puede representarse gráficamente. Por ejemplo, una red social puede representar la estructura de poder dentro de una sociedad al identificar los vínculos (aristas), su dirección e intensidad y da idea de la manera en que el poder se transmite y a quiénes.
Los grafos son importantes en el estudio de la biología y hábitat. El vértice representa un hábitat y las aristas (o "edges" en inglés) representa los senderos de los animales o las migraciones. Con esta información, los científicos pueden entender cómo esto puede cambiar o afectar a las especies en su hábitat.
- Composición:
Un grafo está compuesto por dos conjuntos finitos, un conjunto de |A| aristas y un conjunto de |V| vértices. J es la relación de incidencia, que asocia a cada elemento de |A| un par de elementos de |V|
Se denota G= { A, V, j}
* Vértices: Son los objetos representados por punto dentro del grafo.
* Aristas Adyacentes: dos aristas son adyacentes si convergen sobre el mismo vértice.
* Aristas Múltiples o Paralelas: dos aristas son múltiples o paralelas si tienen los mismos vértices en común o incidente sobre los mismos vértices.
* Lazo: es una arista cuyos extremos inciden sobre el mismo vértice.
- Tipos de grafos:
* No dirigidos: son aquellos en los cuales los lados no están orientados (no son flechas). Cada lado se representa entre paréntesis, separando sus vértices por comas, y teniendo en cuenta (vi,vj)=(vj,vi).
* Dirigidos: son aquellos en los cuales los lados están orientados (flechas). Cada lado se representa entre ángulos, separando sus vértices por comas y teniendo en cuenta <vi ,vj>=<Vj ,vi>. En grafos dirigidos, para cada lado <a,b>, a, el cual es el vértice origen, se conoce como la cola del lado y b, el cual es el vértice destino, se conoce como cabeza del lado.
* Grafo simple. o simplemente grafo es aquel que acepta una sola una arista uniendo dos vértices cualesquiera. Esto es equivalente a decir que una arista cualquiera es la única que une dos vértices específicos. Es la definición estándar de un grafo.
* Grafo etiquetado. Grafos en los cuales se ha añadido un peso a las aristas (número entero generalmente) o un etiquetado a los vértices.
* Grafo aleatorio. Grafo cuyas aristas están asociadas a una probabilidad.
Hipergrafo. Grafos en los cuales las aristas tienen más de dos extremos, es decir, las aristas son incidentes a 3 o más vértices.
* Grafo infinito. Grafos con conjunto de vértices y aristas de cardinal infinito.
- Representación de grafos:
Existen diferentes formas de representar un grafo (simple), además de la geométrica y muchos métodos para almacenarlos en una computadora. La estructura de datos usada depende de las características del grafo y el algoritmo usado para manipularlo. Entre las estructuras más sencillas y usadas se encuentran las listas y las matrices, aunque frecuentemente se usa una combinación de ambas. Las listas son preferidas en grafos dispersos porque tienen un eficiente uso de la memoria. Por otro lado, las matrices proveen acceso rápido, pero pueden consumir grandes cantidades de memoria.
* Estructura de lista
- Lista de incidencia - Las aristas son representadas con un vector de pares (ordenados, si el grafo es dirigido), donde cada par representa una de las aristas.
- Lista de adyacencia - Cada vértice tiene una lista de vértices los cuales son adyacentes a él. Esto causa redundancia en un grafo no dirigido (ya que A existe en la lista de adyacencia de B y viceversa), pero las búsquedas son más rápidas, al costo de almacenamiento extra.
- Lista de grados - También llamada secuencia de grados o sucesión gráfica de un grafo no-dirigido es una secuencia de números, que corresponde a los grados de los vértices del grafo.
* Estructuras matriciales:
- Matriz de adyacencia - El grafo está representado por una matriz cuadrada M de tamaño n^2, donde n es el número de vértices. Si hay una arista entre un vértice x y un vértice y, entonces el elemento m_{x, y} es 1, de lo contrario, es 0.
- Matriz de incidencia - El grafo está representado por una matriz de A (aristas) por V (vértices), donde [arista, vértice] contiene la información de la arista (1 - conectado, 0 - no conectado)
- Ciclos y caminos:
Un ciclo es una sucesión de aristas adyacentes, donde no se recorre dos veces la misma arista, y donde se regresa al punto inicial.
Un ciclo hamiltoniano tiene además que recorrer todos los vértices exactamente una vez (excepto el vértice del que parte y al cual llega).
Por ejemplo, en un museo grande (al estilo del Louvre), lo idóneo sería recorrer todas las salas una sola vez, esto es buscar un ciclo hamiltoniano en el grafo que representa el museo (los vértices son las salas, y las aristas los corredores o puertas entre ellas).
Se habla también de camino Hamiltoniano si no se impone regresar al punto de partida, como en un museo con una única puerta de entrada. Por ejemplo, un caballo puede recorrer todas las casillas de un tablero de ajedrez sin pasar dos veces por la misma: es un camino hamiltoniano. Ejemplo de un ciclo hamiltoniano en el grafo del dodecaedro.
- Grafos planos:
Cuando un grafo o multigrafo se puede dibujar en un plano sin que dos segmentos se corten, se dice que es plano.
Un juego muy conocido es el siguiente: Se dibujan tres casas y tres pozos. Todos los vecinos de las casas tienen el derecho de utilizar los tres pozos. Como no se llevan bien en absoluto, no quieren cruzarse jamás. ¿Es posible trazar los nueve caminos que juntan las tres casas con los tres pozos sin que haya cruces?
Cualquier disposición de las casas, los pozos y los caminos implica la presencia de al menos un cruce.
Sea Kn el grafo completo con n vértices, Kn, p es el grafo bipartito de n y p vértices.
El juego anterior equivale a descubrir si el grafo bipartito completo K3,3 es plano, es decir, si se puede dibujar en un plano sin que haya cruces, siendo la respuesta que no. En general, puede determinarse que un grafo no es plano, si en su diseño puede encontrase una estructura análoga (conocida como menor) a K5 o a K3,3.
Establecer qué grafos son planos no es obvio, y es un problema que tiene que ver con topología.
Fuentes:
Aplicaciones de matrices
Dominar las matrices puede ser frustrante para cualquier estudiante de álgebra. Entre escribirlas apropiadamente y realmente resolverlas, el proceso puede ser causa de confusión. Sin embargo, como la mayoría de los conceptos matemáticos, resistir el proceso de aprendizaje puede ser mucho más sencillo cuando sabes exactamente cómo esos cálculos se aplican a la vida cotidiana. Aprender acerca de las matrices no es diferente, y afortunadamente, los conceptos detrás de las matrices se aplican de forma regular en la vida diaria.
- Cálculo del área de un triángulo:
Mientras que el área de un triángulo puede ser fácilmente calculada cuando éste es un triángulo rectángulo, si los ángulos son más complicados, ésto puede significar un cálculo más difícil. Si las longitudes de los lados de un triángulo son desconocidas, entonces el problema puede resolverse mediante matrices y determinantes. Este método típicamente involucra usar una forma simple de la regla de Cramer, aunque también se puede aplicar a problemas que requieren una versión extendida de la regla (como por ejemplo, en una matriz de 3x3).
- Análisis de una caja negra:
Más aplicable en el campo de la ingeniería que en ninguna otra área de estudio, las matrices se pueden usar para resolver problemas de circuitos que involucran a voltajes de entrada y salida. Esto normalmente requiere un cálculo simple en una matriz de 2x2. Para resolver estos problemas, debes conocer los componentes del circuito (resistencias, amplificadores operativos, capacitores, etc), y el voltaje de entrada. Las corrientes y el voltaje de salida se pueden descubrir a través de una aplicación de matemática matricial.
- Predicciones de marketing:
Las matrices no sólo son aplicadas por ingenieros y matemáticos. Los analistas de negocios también deben tener un conocimiento básico de matrices cuando trabajan en análisis del mercado y de los precios. La forma de matrices que se usa para este tipo de cálculos depende del análisis que se realiza, y puede ir desde una matriz de 3x4 hasta una matriz rectangular mucho más grande. Para todos los tamaños, sin embargo, el análisis de mercado se realiza de la misma forma, sólo que en distinta escala.
- Cifrado / Codificación:
Las matrices se usan regularmente en todas las formas de cifrado, tanto en programación de computadoras como en criptología. Para la programación, se usan arreglos de dos dimensiones para incluir la información necesaria de las matrices relevantes. A la hora de codificar mensajes, el mensaje enviado depende del código de la matriz detrás del sistema del mensaje. La persona que lo recibe debe conocer la matriz original para poder descifrar el mensaje acertadamente.
Fuente:
Resolución de sistemas con matrices II
- Método de Crammer:
Un sistema de ecuaciones lineales recibe el nombre de sistema de Cramer cuando se cumplen las dos condiciones siguientes:
1) El número de ecuaciones es igual al número de incógnitas.
2) El determinante de la matriz de los coeficientes (matriz del sistema) es distinto de cero ( det ( A ) # 0 )
Un sistema de Cramer es, por definición, compatible determinado, puesto que se cumple que rango (A) = rango (A*) = n (nº de incógnitas).
Consideremos un sistema de Cramer, es decir, un sistema de n ecuaciones lineales con n incógnitas, cuya expresión general es la siguiente:
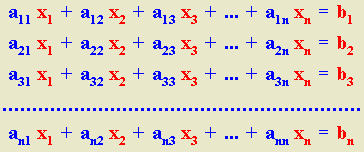
Todos los sistemas de Cramer son compatibles determinados.
El valor de cada incógnita se obtiene dividiendo el determinante de la matriz
asociada a dicha incógnita por la matriz del sistema (matriz de los
coeficientes de las incógnitas).

Ejemplo:



Un sistema de Cramer es, por definición, compatible
determinado. Pero, ¿Se puede aplicar la regla de Cramer para resolver sistemas
de ecuaciones lineales compatibles indeterminados?
La respuesta es también afirmativa. El procedimiento a
seguir es el siguiente: Supongamos que tenemos un sistema de m
ecuaciones lineales con n incógnitas, tal que: rango (A) = rango (A*) = k < n. Por lo
tanto, sobran m - k ecuaciones y, además, hay n - k
incógnitas no principales. Para averiguar cuáles son las ecuaciones de
las que podemos prescindir, y cuáles son las incógnitas no principales, basta
encontrar en la matriz de los coeficientes ( A ) un menor de orden k
distinto de cero, por ejemplo, el que utilizamos para averiguar el rango
de la matriz A. Las filas que
intervienen en este menor son las que corresponden a las ecuaciones principales
o independientes. Las restantes ecuaciones las podemos suprimir. Las columnas
que figuran en dicho menor corresponden a las incógnitas principales. Las
incógnitas no principales las pasamos al otro miembro y pasan a formar un único
término junto con el término independiente. Se obtiene, de este modo, un
sistema de k ecuaciones lineales con k
incógnitas, cuyas soluciones van a depender de n - k
parámetros (correspondientes a las incógnitas no principales).
- Teorema de Rouché:
Permite conocer si un sistema de ecuaciones tiene solución a partir del estudio del
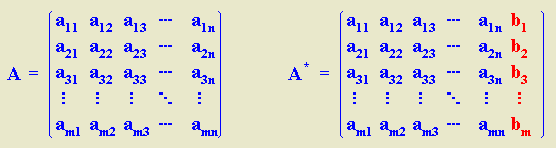
rango de la matriz asociada al sistema (matriz de coeficientes A) y del rango de la matriz
ampliada de éste (matriz B).
rango de la matriz asociada al sistema (matriz de coeficientes A) y del rango de la matriz
ampliada de éste (matriz B).

Sea A la matriz de coeficiente asociada a un sistema lineal de n.
Sea A* la matriz ampliada de dicho sistema, se cumple q:
1) Si Rg (A) no es igual a Rg (A*): S.I. (no existe solución)
2) Si Rg (A)=Rg (A*)=n: S.C.D. (existe una única solución)
3) Si Rg (A)=Rg (A*)<n: S.C.I. (existe infinitas soluciones)
Un caso particular es el de los sistemas homogéneos, es decir, aquellos en los que todos los términos independientes son nulos. Pues, en este caso, las matrices A y A* son semejantes a efectos del cálculo del rango, dado que la matriz A* es la matriz A a la que se le añade una columna de ceros, que podemos suprimir para calcular el rango. Por lo tanto, siempre se cumple que rango (A) = rango (A*). Esto quiere decir que todos los sistemas homogéneos son siempre compatibles. Se cumple:
1) Si rango (A) = n (número de incógnitas), el sistema es compatible determinado. Tiene una única solución, que se conoce con el nombre de solución trivial. Es aquella en la que todas las incógnitas son nulas ( 0 ).
2) Si rango (A) < n (número de incógnitas), el sistema es compatible indeterminado (tiene infinitas soluciones).
Una vez realizada la "discusión o identificación del sistema", aplicaremos alguno de los métodos que desarrollaremos en los epígrafes posteriores. No obstante, es preciso tener en cuenta las siguientes observaciones:
1) Si el sistema es compatible determinado, el valor común de los rangos indica el número de ecuaciones principales, es decir, aquellas que no dependen de las restantes.
2) Si el sistema es compatible indeterminado, (rango (A) = rango (A*) = k < n) el valor común de los rangos ( k ) indica tanto el número de ecuaciones independientes o principales, como el número de incógnitas principales. Las restantes incógnitas (no principales) n - k las pasaremos al segundo miembro formando un único término junto al término independiente. Siguiendo este procedimiento obtendremos un sistema de k ecuaciones lineales con k incógnitas (principales), al que aplicaremos uno de los procedimientos que estudiaremos en los siguientes apartados: Regla de Cramer, Método de Gauss o, por la matriz inversa.
- Resolución de sistema homogéneos:
Sabemos que un sistema es homogéneo si todos los términos
independientes son
cero, y que además, estos sistemas son siempre compatibles.
Aplicando el Teorema de Rouché-Frobenius:
1) Si Rang(A)= nº de incógnitas Î S.C.D. Solución trivial.
(0,0,0).
2) Si Rang(A)< nº de incógnitas Î S.C.I. Infinitas
soluciones, entre ellas la (0,0,0).
Fuente:
Mis apuntes
Resolución de sistemas con matrices I
El objetivo de este apartado es examinar los aspectos numéricos que se presentan al resolver sistemas de ecuaciones lineales de la forma:
Se trata de un sistema de n ecuaciones con n incógnitas, x1, x2, ..., xn. Los elementos aij y bi son números reales fijados.
El sistema de ecuaciones se puede escribir, empleando una muy útil representación matricial, como:
Entonces podemos denotar estas matrices por A, x y b de forma que la ecuación se reduce simplemente a:
| Ax=b |
Los métodos de resolución de sistemas de ecuaciones se pueden dividir en dos grandes grupos:
- Los Métodos exactos o algoritmos finitos que permiten obtener la solución del sistema de manera directa.
- Los Métodos aproximados que utilizan algoritmos iterativos e infinitos y que calculan las solución del sistema por aproximaciones sucesivas.
De entre los métodos exactos analizaremos el método de Gauss y una modificación de éste denominado método de Gauss-Jordan. Entre los métodos aproximados nos centraremos en el estudio de los métodos de Richardson, Jacobi y Gauss-Seidel.
- Método de eliminación para resolver sistemas de ecuaciones lineales de Gauss - Jordan:
Para resolver un sistema de ecuaciones con este método se emplea la eliminación sucesiva de las incógnitas según este esquema: Considere las siguientes m ecuaciones lineales:
Ahora se arregla una matriz B de este sistema, ampliada con los bi (línea vertical).
Después se hacen transformaciones elementales con los renglones de la matriz, lo cual es equivalente a hacerlo con las respectivas ecuaciones:
- Se permite cambiar el orden de las filas.
- Se pueden multiplicar los renglones por cualquier número diferente de cero.
- Sumar a un renglón de la matriz, otra fila multiplicada por cualquier número.
Así se obtiene una matriz ampliada de un nuevo sistema equivalente al original pues se reduce la matriz B a la forma más sensilla posible que incluya la solución del sistema. A continuación se presenta el procedimiento detallado:
- Intercambio de ecuaciones y de la posición de las incógnitas para que a11
 0.
0. - Multiplicación de la primera ecuación por una constante apropiada diferente de cero, para lograr a11 = 1.
- Para toda i > 1, se multiplica la primera ecuación por -ai1 y luego se suma a la i-ésima ecuación, de tal manera que la primera incógnita queda eliminada.
Considere el siguiente ejemplo con anotaciones del cálculo a la izquierda:
La matriz ampliada de este sistema es:
Se resta: el renglón (1) del (2) y el (3), el (1)(3) al (4), resultando la matriz:
Se permutan los renglones (2) y (3) para tener el coeficiente 1en renglón 2
El renglón (2) se duplica y se resta al (1) y al (4), el (2) se triplica y se resta al (3)
El (3) se divide entre (-14), el coeficiente 1 resultante se usa para operar con el cálculo que se indica en la columna izquierda
La columna derecha de la última matriz tiene la solución del sistema propuesto: X1 = -1, X2 = 0, X3 = 1
Ecuacion lineal degenerativa.- Así llamada cuando todos los coeficientes de las incógnitas son cero. En el caso especial de un sistema en que todas las ecuaciones son degenerativas ( aij = 0), se tienen dos casos:
aij = 0), se tienen dos casos:
 aij = 0), se tienen dos casos:
aij = 0), se tienen dos casos:- El sistema tiene por lo menos una ecuación de la forma: 0x1 + 0x2 +...+ 0xn = bi con bi
 0, entonces esta ecuación y por lo tanto el sistema, no tiene solución, (es inconsistente).
0, entonces esta ecuación y por lo tanto el sistema, no tiene solución, (es inconsistente). - Todas las ecuaciones del sistema son de la forma: 0x1 + 0x2 +...+ 0xn = 0, entonces cada ecuación y, por lo tanto el sistema tienen toda "n-ada" de números reales como solución.
En el caso común cuando las ecuaciones no son todas degenerativas (aij  0), el sistema de ecuaciones se reduce a uno más simple equivalente al original que posee las mismas soluciones, el proceso se lleva hasta eliminación completa (Gauss-Jordan) para obtener la solución.
0), el sistema de ecuaciones se reduce a uno más simple equivalente al original que posee las mismas soluciones, el proceso se lleva hasta eliminación completa (Gauss-Jordan) para obtener la solución.
 0), el sistema de ecuaciones se reduce a uno más simple equivalente al original que posee las mismas soluciones, el proceso se lleva hasta eliminación completa (Gauss-Jordan) para obtener la solución.
0), el sistema de ecuaciones se reduce a uno más simple equivalente al original que posee las mismas soluciones, el proceso se lleva hasta eliminación completa (Gauss-Jordan) para obtener la solución.
Si se encuentra una ecuación de la forma 0x1 +... +0xn = 0 puede quitarse sin que afecte la solución.
Continuando con el proceso anterior, con cada nuevo subsistema, se obtiene por inducción, que el sistema o bién no tiene solución, ó bien es reductible a una forma equivalente.
Para la solución de un sistema de ecuaciones lineales en forma escalonada (eliminación de Gauss-Jordan), hay dos casos:
- Si hay tantas ecuaciones como incógnitas (m-=n) entonces el sistema tiene una solución única.
- Si hay menos ecuaciones que incógnitas (m < m + n) entonces se pueden asignar arbitrariamente valores a las n variables llamadas en este caso "libres" y obtener una solución del sistema. Si se asignan valores diferentes a tales "variables libres", se pueden obtener muchas soluciones del sistema.
Para el caso particular de un sistema homogéneo de ecuaciones lineales reducido a la forma escalonada se presentan dos posibilidades.
1)Tantas ecuaciones como incógnitas (m = n), entonces la solución es (0, 0,.....0) ó trivial.
2) Menos ecuaciones que incógnitas (m < m + n), entonces el sistema tiene una solución no nula. En resumen:
- Método de Richardson:
El método de Richardson toma como matriz Q la matriz identidad (I). En este caso la ecuación queda en la forma:| Ix(k) = (I-A)x(k-1)+b = x(k-1)+r(k-1) |
en donde r(k-1) es el vector residual definido mediante r(k-1)=b-Ax(k-1).La matriz identidad es aquella matriz diagonal cuyos elementos no nulos son 1, es decir:

y cumple que
IA = A
para cualquier valor de A; es decir, es el elemento neutro del producto matricial. De acuerdo con esto, la ecuación se puede escribir como:
x(k) = x(k-1) - Ax(k-1) + b = x(k-1) + r(k-1)
en donde un elemento cualquiera del vector r(k-1) vendrá dado por la expresión:

En la siguiente figura se muestra un algoritmo para ejecutar la iteración de Richardson. Este método recibe también el nombre de método de relajación o método de los residuos.
- Método de Jacobi:
En la iteración de Jacobi, se escoge una matriz Q que es diagonal y cuyos elementos diagonales son los mismos que los de la matriz A. La matriz Q toma la forma:
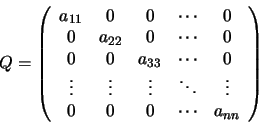
y la ecuación general se puede escribir como
Si denominamos R a la matriz A-Q:

la ecuación anterior se puede reescribir como:
El producto de la matriz Q por el vector columna x(k) será un vector columna. De modo análogo, el producto de la matriz R por el vector columna x(k-1) será también un vector columna. La expresión anterior, que es una ecuación vectorial, se puede expresar por necuaciones escalares (una para cada componente del vector). De este modo, podemos escribir, para un elemento i cualquiera y teniendo en cuenta que se trata de un producto matriz-vector:
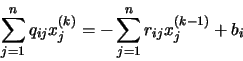
Si tenemos en cuenta que en la matriz Q todos los elementos fuera de la diagonal son cero, en el primer miembro el único término no nulo del sumatorio es el que contiene el elemento diagonal qii, que es precisamente aii. Más aún, los elementos de la diagonal de Rson cero, por lo que podemos eliminar el término i=j en el sumatorio del segundo miembro. De acuerdo con lo dicho, la expresión anterior se puede reescribir como:
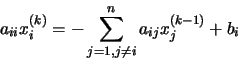
de donde despejando xi(k) obtenemos:
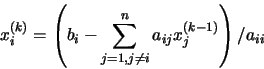
que es la expresión que nos proporciona las nuevas componentes del vector x(k) en función de vector anterior x(k-1) en la iteración de Jacobi. En la figura siguiente se presenta un algoritmo para el método de Jacobi.
El método de Jacobi se basa en escribir el sistema de ecuaciones en la forma:
Partimos de una aproximación inicial para las soluciones al sistema de ecuaciones y sustituimos estos valores en la ecuación anterior. De esta forma, se genera una nueva aproximación a la solución del sistema, que en determinadas condiciones, es mejor que la aproximación inicial. Esta nueva aproximación se puede sustituir de nuevo en la parte derecha de la ecuación anterior y así sucesivamente hasta obtener la convergencia.
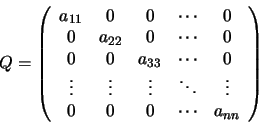
y la ecuación general se puede escribir como
| Qx(k) = (Q-A)x(k-1) + b |
Si denominamos R a la matriz A-Q:

la ecuación anterior se puede reescribir como:
Qx(k) = -Rx(k-1) + b
El producto de la matriz Q por el vector columna x(k) será un vector columna. De modo análogo, el producto de la matriz R por el vector columna x(k-1) será también un vector columna. La expresión anterior, que es una ecuación vectorial, se puede expresar por necuaciones escalares (una para cada componente del vector). De este modo, podemos escribir, para un elemento i cualquiera y teniendo en cuenta que se trata de un producto matriz-vector:
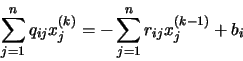
Si tenemos en cuenta que en la matriz Q todos los elementos fuera de la diagonal son cero, en el primer miembro el único término no nulo del sumatorio es el que contiene el elemento diagonal qii, que es precisamente aii. Más aún, los elementos de la diagonal de Rson cero, por lo que podemos eliminar el término i=j en el sumatorio del segundo miembro. De acuerdo con lo dicho, la expresión anterior se puede reescribir como:
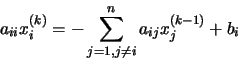
de donde despejando xi(k) obtenemos:
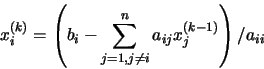
que es la expresión que nos proporciona las nuevas componentes del vector x(k) en función de vector anterior x(k-1) en la iteración de Jacobi. En la figura siguiente se presenta un algoritmo para el método de Jacobi.
El método de Jacobi se basa en escribir el sistema de ecuaciones en la forma:
Partimos de una aproximación inicial para las soluciones al sistema de ecuaciones y sustituimos estos valores en la ecuación anterior. De esta forma, se genera una nueva aproximación a la solución del sistema, que en determinadas condiciones, es mejor que la aproximación inicial. Esta nueva aproximación se puede sustituir de nuevo en la parte derecha de la ecuación anterior y así sucesivamente hasta obtener la convergencia.
- Método de Gauss-Seidel:
La iteración de Gauss-Seidel se define al tomar Q como la parte triangular inferior de A incluyendo los elementos de la diagonal: 
Si, como en el caso anterior, definimos la matriz R=A-Q

y la ecuación se puede escribir en la forma:
Qx(k) = -Rx(k-1) + b
Un elemento cualquiera, i, del vector Qx(k) vendrá dado por la ecuación:
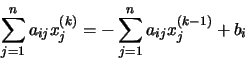
Si tenemos en cuenta la peculiar forma de las matrices Q y R, resulta que todos los sumandos para los que j > i en la parte izquierda son nulos, mientras que en la parte derecha son nulos todos los sumandos para los que
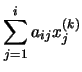 | = | 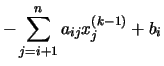 | |
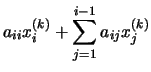 | = | 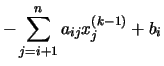 |
de donde despejando xi(k), obtenemos:
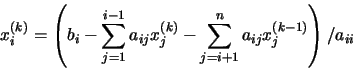
Obsérvese que en el método de Gauss-Seidel los valores actualizados de xi sustituyen de inmediato a los valores anteriores, mientras que en el método de Jacobi todas las componentes nuevas del vector se calculan antes de llevar a cabo la sustitución. Por contra, en el método de Gauss-Seidel los cálculos deben llevarse a cabo por orden, ya que el nuevo valor xi depende de los valores actualizados de x1, x2, ..., xi-1.
En la figura siguiente se incluye un algoritmo para la iteración de Gauss-Seidel.
Fuente:
http://148.204.211.134/polilibros/portal/Polilibros/P_Terminados/Investigacion_de_Operaciones_Careaga/Common/IO-apendicea-eqlinealesgaussjordan.htm
http://www.uv.es/~diaz/mn/node25.html
http://www.uv.es/~diaz/mn/node34.html
http://www.uv.es/~diaz/mn/node35.html
http://www.uv.es/~diaz/mn/node36.html
Suscribirse a:
Entradas (Atom)